Basic Random Variabel

Pada tutorial ini penulis akan menjelaskan dasar - dasar dari random variabel. Dimulai dengan "probability" atau kemungkinan. Dikarenakan random variabel mempunyai nilai yang tidak diketahui (bersifat random) maka biasanya dihitung berdasarkan nilai statistik. Salah satu nilai statistik tersebut adalah "Probability Density Function" p(x) yang didefinikan sebagai berikut,

Ini berarti terdapat kemungkinan x akan muncul antara -infinity (minus tak hingga) dan infinity (tak hingga).

Kemudian "Probability Distribution Function" yang merupakan integral dari "probability density function".

Dan "mean" atau "expected value" didefinisikan sebagai berikut,

Kita juga bisa mengartikan persamaan diatas sebagai nilai mean dari jumlah (integral) semua nilai x yang dikalikan dengan probability. Nilai "mean squared" dari x adalah,

Kemudian "variance" dari random variabel adalah ukuran yang menentukan seberapa besar random variabel akan bervariasi terhadap nilai mean. Variance didefinikan sebagai berikut,

Dan standard deviasi juga menentukan seberapa besar random variabel akan bervariasi terhadap nilai mean yang didefinikan tanpa kuadrat sebagai berikut,

Jika kita mempunyai "independent random variabel"  maka nilai variance adalah jumlah dari variance masing - masing x sebagai berikut,

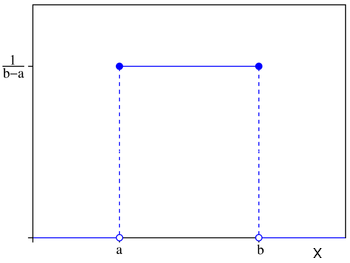
Contoh dari "probability density function" adalah "uniform distribution" yang ditunjukkan seperti gambar berikut. Dengan "probability density function" semua nilai x antara a dan b mempunyai kesempatan yang sama untuk terjadi / muncul.

Nilai mean dari grafik diatas adalah

dan nilai variance adalah sebagai berikut,

Ini berarti jika random variabel bervariasi antara 0 dan 1, maka nilai mean adalah 1/2 dan nilai variance adalah 1/12. Contoh untuk mendapatkan variance = 1 dengan menggunakan uniform distribusi bisa dilakukan dengan menjumlahkan nilai random antara 0 dan 1 sebanyak 12 kali. Pada akhir tutorial penulis akan memberikan contoh bagaimana men-generate gaussian random.

Contoh dari "probability distribution function" adalah "Gaussian Normal Distribution" yang mempunyai zero mean. Biasanya "gaussian" digunakan untuk memberi noise pada sensor. Gaussian mempunyai persamaan sebagai berikut,

Dengan m dan sigma adalah parameter. Berikut adalah grafik gaussian.

Dari grafik dapat diketahui nilai mean E(x) = m. Dan mempunyai variance . Grafik akan nol jika melebihi 3 standard deviasi (). 68% probability untuk satu standard deviasi dan 95% untuk dua standard deviasi.

Pada listing program di bawah adalah program untuk men-generate gaussian random menggunakan C code. Hal yang perlu dicermati adalah C code mempunyai library untuk fungsi random yaitu rand(). Fungsi ini akan men-generate nilai random menggunakan "Uniform Distribution" antara 0 sampai 32767.

Terlebih dahulu kita harus me-normalisasikan nilai rand(), disini penulis akan menormalisasikan nilai random antara -0.5 sampai 0.5. Maka hasil dari fungsi rand() akan kita bagi dengan 32767 kemudian mengurangkan dengan 0.5.

Dari persamaan diatas yaitu untuk "uniform distribution" kita ketahui mempunyai variance 1/12 untuk nilai random antara 0 sampai 1. Hal ini juga sama untuk -0.5 sampai 0.5. Untuk mendapatkan nilai variance = 1 maka nilai random variabel perlu dijumlahkan sebanyak 12 kali. Jika kita menjumlahkan nilai random sebanyak 6 kali maka akan didapat nilai variance = 1/2. Untuk itu kita harus mengalikannya dengan akar 2 yaitu 1.414 untuk mendapatkan variance = 1. Akar 2 diperoleh dari variance yang dijumlahkan seperti berikut,

float GaussRandom(float scale)
{
    float sum, ran;
    int i;     

    sum = 0.0f;
    for (i=0; i<6; i++)
    {
        ran = (float)rand();
        ran = (ran / 32767) - 0.5;
        sum = sum + ran;
    }

    return (1.414f * sum * scale);
}

Sekian tutorial ini, semoga bermanfaat. ^^ Jangan lupa untuk disebarkan ke teman - teman anda.