Tutorial for Everyone: Norm (Mathematics)

Menurut wikipedia 'norm' adalah suatu fungsi yang memberikan ukuran panjang atau size pada semua vektor dalam sebuah vektor space. Sebagai contoh dua dimensi Euclidean norm; Elemen pada vektor space ini biasanya digambarkan dengan sebuah anak panah pada bidang kartesian dua dimensi yang dimulai pada origin (0,0). Panjang pada anak panah ini menunjukkan Euclidean norm. Oleh karena itu, Euclidean norm disebut sebagai 'magnitude' atau besaran dari vektor.

Kadangkala kita membutuhkan suatu nilai skalar untuk mengukur suatu besaran dari vektor atau matrik, maka kita membutuhkan norm.

Norm pada linear algebra banyak dijumpai ketika anda mendesain dengan menggunakan H infinity kontrol. Norm yang digunakan adalah norm-infinity.

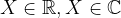Untuk vektor $\dpi{120} x=[x_1,x_2,...,x_m]^T \quad x\in X$ , dengan X adalah vektor space dan $\dpi{120} X\in\mathbb{R}, X\in\mathbb{C}$ , maka norm dari vektor space x adalah 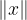$\dpi{120} \left \| x \right \|$ . Berikut adalah tiga syarat agar bisa dikualifikasikan sebagai norm,

Untuk $\dpi{120} \forall x \in X,\left \| x \right \|\geq 0$ dengan $\dpi{120} \left \| x \right \|= 0,x=0$ atau zero vektor.
Untuk $\dpi{120} \forall x \in X$ dan semua $\dpi{120} \alpha \in \mathbb{F},\left \| \alpha x \right \|=\left | \alpha \right |\left \| x \right \|$ .
(Triangle inequality) $\dpi{120} \forall x_1,x_2 \in X$ maka $\dpi{120} \left \| x_1+x_2 \right \|\leq \left \| x_1 \right \|+\left \| x_2 \right \|$

Norm didefinisikan sebagai berikut, misal $\dpi{120} x=[x_1,x_2,...,x_m]^T \quad x\in X$ maka p-norm adalah sebagai berikut,

$\dpi{120} 1-\text{norm}\quad \left \| x \right \|_1 :=\sum _{i=1}^m\left | x_i \right |,\quad for \quad p=1 \\ p-\text{norm}\quad\left \| x \right \|_p := (\sum_{i=1}^m\left | x_i \right |^p)^{\frac{1}{p}},\quad for \quad 1<p<\infty \\ \infty-\text{norm}\quad \left \| x \right \|_{\infty}:=\text{max}_{1\leq i\leq m}\left | x_i \right |,\quad for\quad p=\infty$

Misal p=2, maka 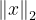$\dpi{120} \left \| x \right \|_2$ adalah norm yang sudah kita kenal yaitu Euclidean norm. Norm ini mengukur besaran suatu vektor atau panjang vektor.

Jika x adalah variable yang berubah terhadap waktu x(t), maka p-norm x(t) didefinikan sebagai berikut,

$\dpi{120} 1-norm \quad \left \| x \right \|_1 :=\int_{-\infty}^{\infty}\left | x(t) \right |dt,\quad for \quad p=1 \\ p-norm \quad \left \| x \right \|_p := \left ( \int_{-\infty}^{\infty}\left | x(t) \right |^p dt \right ) ^{1/p}, \quad for \quad 1<p<\infty \\ \infty - norm \quad \left \| x \right \|_{\infty}:=\text{sup}_{t\in\mathbb{R}}\left | x(t) \right |,\quad for \quad p=\infty$

$\dpi{120} \text{sup}_{t\in\mathbb{R}}[.]$ adalah supremum fungsi, yang menunjukkan nilai terbesar dari fungsi yang berada dalam tanda braket [ dan ] ketika t bervariasi terhadap waktu. Misal kita mempunyai vektor x=(1, 2, 3) maka,

$\dpi{120} 1-norm\quad\left \| x \right \|_1=6 \\ 2-norm\quad\left \| x \right \|_2=\sqrt{14} \\ 3-norm\quad\left \| x \right \|_3=6^{2/3} \\ \infty-norm\quad\left \| x \right \|_{\infty}=3$

Yang terakhir adalah tentang sistem norm. Sebenarnya sistem norm adalah gain input-output pada sistem. Misal G adalah gain linear sistem dengan u(t) adalah input signal dan y(t) adalah output signal. Dimana $\dpi{120} u\in(U,\left \| . \right \|_U),y\in(Y,\left \| . \right \|_Y)$ . U dan Y adalah signal space. Kemudian norm, maximum sistem gain adalah sebagai berikut.

$\dpi{120} \left \| G \right \|=\text{sup}_{u\neq 0}\frac{\left \| Gu \right \|_Y}{\left \| u \right \|_U}$

Sekian dari tutorial ini, smoga bermanfaat.. amiinn..^^

Tutorial for Everyone

Pages

Saturday, May 26, 2012

Norm (Mathematics)

4 comments: